川ブームも今は昔
はじめに
前回、幅1の部屋が連なった通称「川」の仕掛けについて、解説を行いました。
要点だけ軽くまとめると
- 黒マスのつながり・アースを意識すると考えやすい
- 川の中の黒マス・白マスは、おおむね境界線に垂直な方向に3マス向こうにコピーされる(詳しい条件は割愛)
- 角の幅3の川については、川の側面に接しただけで、盤面端にもアースしてしまう(角の川定理)
という感じ。特に最後の角の川定理はよく使うので、もう一度主張を書いておきます:
角の川定理
図のように、長さ n で 3 本の川が盤面の角に接しているとき、この幅 4 * n の長方形内の黒マスは、この中だけでアースする。なお、川の長さ n によらず成立する。

さらに、角の川定理の適用例として紹介した、代表的なハタンパターンも載せておきます。


よりくわしい説明や定理の証明は、元の記事を参照してください。
さて今回は、川を利用した自作のへやわけの中から、何問かピックアップして解説を行いたいと思います。角の川定理を手筋としてどう使いこなせばいいか、ぜひ参考にしてください!
↑ Puzzle Squareに上げた自作へやわけ。こう見るとほとんど川だなぁ。
記法
解説で使うマスの記法について
左上のマスを1行1列目として、x行y列目のマスを "RxCy" と表します。たとえば、R3C2は3行2列目のマスのことです。

問題解説
1. オーソドックスな分断回避
まずはこの問題から。

リンクは以下:
左上に川の構造があり、半分接するように3の部屋があります。3の部屋のパターンは2通りありますが、黒マスが川に接してしまうパターンは、角の川定理により左上に引き込まれて分断が起きてしまいます。

よってもうひとつのパターンに確定します。
またそのあとも川による分断回避が起きます。具体的には、R4C3やR3C4も白でないといけません。次の図のように黒くなると、やはり左上に接地します。


あとは黒マスの伝播を意識すると埋まります。川の内部の黒マスを決める詰めの部分は似たような議論になることが多いので、慣れるとサクサク埋められると思います。
練習問題として次を挙げておきます。
2の廊下の部屋で分断回避を考えましょう。そのあとも黒マスの個数や分断を意識すると解けると思います。
2. 不完全な川
さっきの応用がこちら

前の問題と似ていますが、違いとして
- 左上の川が不完全
- 3の部屋がどっちのパターンでも川に接地してしまう
ということが分かります。
特に不完全なことがポイントで、R1C1とR2C1の間の境界があれば、完全な角の川となってハタンしてしまいます。

境界が増えたことで追加された条件は「R1C1, R2C1, R3C1のいずれかが黒マスになる」というものなので、翻って元の問題では、この否定である「R1C1, R2C1, R3C1の全てが白マスである」という条件が成り立つ必要があります。

加えて、R4C1に発生した黒マスから川の内部(R3C2)に黒マスが伸びるのもハタンします。この説明はやや難しいのですが、3の部屋起因の黒マスのつながりについて、左上でのアースを回避するために必要です。R3C2に黒マスがあると、3列目がどんな形であれアースしてしまいます。

結果として、1, 2列目が以下のように決まります。不完全な川の内部で分断を回避するときによくある議論・形だと思います。

この後は、R4C3白・R6C5白・R2C5白・R2C6白などから3の部屋のパターンが決まり解決します。特に後ろの二つは、黒マスの場合に軽い先読みを行うとハタンすることが分かります。詳しくは省略するので、興味があれば実際に盤面で追ってみてください。
ちなみに、先読みをすることもあって、6x6という小さいサイズでもアゼンの難易度としました。ただじゅうぶん理詰めで解ける・論理的に解ける範囲だと思います。
3. 2つの川

この問題では左上と右下に幅3の川があって互いに接しています。
その影響で、接点の近辺であるR3C4, R4C3, R4C4に黒マスがあると、左上・右下にそれぞれ接地してハタンしてしまいます。真ん中の図はR3C4にが黒マスの場合のイメージです。



この3マスの白が分かれば、あとはそれぞれの川への分断回避を考えて埋めることができます。
練習問題です。
まずは先ほどの不完全な川とのミックス問題。
右下が不完全な川ですが、完全だとハタンすることが分かります。なのでその周辺で分断を回避しましょう。
次にサイズが増えたバージョン。見た目がシンプルで、取っ掛かりがないようにも見えます。
これも左上と右下に幅3の川があると思え、4行目のいくつかが白マスになると分かります。
あとは2をどう使うか。実は右下の川単体でR5C2が白とわかり、上に伝播してR2C2も白になります。すると2の部屋の黒マスが全然足りず、大まかな配置を確定できます。
さらにこんなのも。
左右で同じ配置になるへやわけ[linked]という変種ですが、考え方は同じです。2つの盤面に隠された川を見つけ出しましょう。
4. 川と黒マス充填
川は接地を誘発するので、黒マスが充填された形と相性がいいです。

この問題は分割充填法を駆使して埋めていくことができます。分割充填についてはゆずっこさんの記事が参考になります:
問題に戻って、初手は辺の5の部屋。これは左下の川の影響で、実質的に角の部屋の5 in 3x4と同じ挙動をとります。中央で3x2の部屋二つに割ったとき、左が3になるとハタンです。よって左2・右3の内訳になります。加えて角の5と同じ議論で右の盤面まで進みます。


次に4の部屋を2x2の部屋3つに区切りましょう。すると、左と中央の2x2の部屋に黒マス2個が入ることはあり得ません。特に中央の部屋については、下の2x3と合わせて、川経由で分断してしまうことに注意しましょう。



結果として、右の2x2に黒マスが2個入ることになります。すると、2の部屋について列目がすべて白マスとなります。これはいずれも、黒マスならば川に接地するためです。
よって2の部屋の中身が決まり、後は自然に埋まっていきます。
練習問題です。
ほぼ同じ議論で解けます。6の部屋に注目したあと、その下の4と2の部屋に注目しましょう。
5. 中央の川による連結
中央の川については現時点で仕組みが解明されていませんが、分断が伝播することは利用することができます。

盤面を見ると、左下と右上の幅3の川が中央の幅5の川でつながっているように見えます。この中央の川がいかに黒マスを伝播させるかがポイントです。
R6C5に注目しましょう。ここが黒マスだとすると、中央の川により、左右の川へと黒マスが伝播してしまいます。よって角の川2つを使ってアースし分断してしまいます。
なのでR6C5は白くないといけません。同様にR6C6も白です。
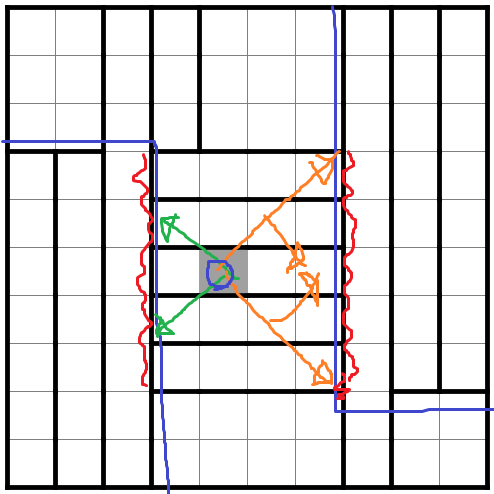

するとその上下2x2マスにおいて黒マスが2個ずつ入ります。
このうち片方のパターンはまた左右に黒マスが伝播してハタンします。よって中央の黒マスパターンが確定します。


このあとも、角の川による分断を回避するよう進めていくことができます。
練習問題。
同じような形ですが、深い二択仮定が必要なのでハバネロにしています。
やはり中央の川のど真ん中は白になるのですが、その上下どちらが黒マスになるのか、黒マスの「抜け方」を意識して確かめてみましょう。
おわりに
以上、川を使った問題の解説でした。
川の論理・手筋の使い方について理解が深まれば幸いです。
また、仕掛けとして面白いと思うので、へやわけを作るときにぜひ仕込んでみてください。